rerooting / 全方位木 DP
因為最近打 ucup 遇到(有人抱怨他不會)所以想說就來簡單寫一篇小科普。
大方向來說,前提是根固定時,問題可以用簡單的樹 DP 解決,然後使用換根 DP 的技巧就可以快速計算出「對於所有 $i$,點 $i$ 當根時候的答案」。
Description
例題: https://atcoder.jp/contests/dp/tasks/dp_v
給定一棵 $N$ 個點的樹。對於每個點 $i$,輸出有幾種把 $N$ 個頂點都塗成黑色或白色的方式,使得所有黑色頂點連通,且頂點 $i$ 是黑色的。
$2 \leq N \leq 10^5$
Solution
我們可以先考慮如果只要輸出 $i = 1$ 的答案該怎麼辦。
相信大家都會簡單的樹上連通塊的 DP:令 $dp_u$ 代表 $u$ 的子樹裡面有幾種塗色方式使得黑色是一個連通塊且這個子樹的根 $u$ 是黑色的。在一個合法的塗色方案當中,$u$ 已經固定是黑色,而 $u$ 的每個小孩 $v$ 都有兩種情形:黑色或白色,如果是黑色的話方案數是 $dp_v$,若是白色則 $v$ 這個子樹固定是全白的,方案數是 $1$。寫下來就是
$$
dp_u = \prod\limits _ {v \in child(u)} (1 + dp_v)
$$
接著,如果根從 $1$ 變成 $x$ 了之後,哪些點的 DP 值有變呢?從下面的圖我們可以發現,因為 DP 值是對整個子樹定義的,而圖中紅色和藍色的節點對應的子樹完全沒有變化,所以其實只有 $1$ 和 $x$ 這兩個點的 DP 值有可能會有變化!
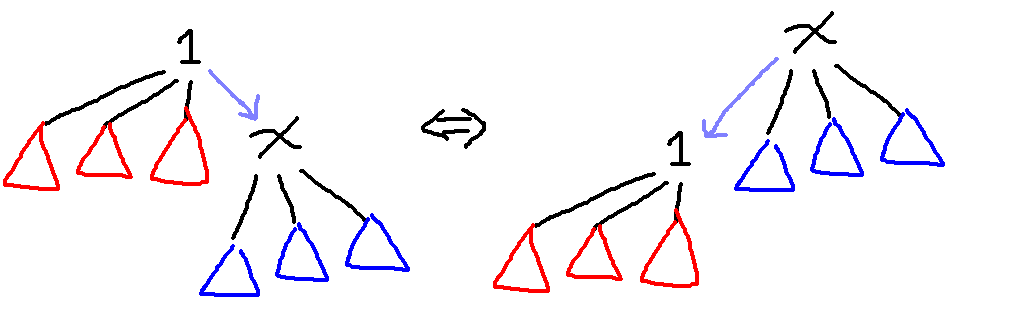
當根從 $x$ 變成一個 $x$ 的鄰居 $y$ 的時候,只有 $x, y$ 兩個頂點的 DP 值會變化,具體來說會像是
$$
\begin{cases}
dp’_x = dp _ x \cdot \frac{1}{ 1 + dp_y } \\
dp’_y = dp _ y \cdot (1 + dp’_x)
\end{cases}
$$
因此,我們可以先 DFS 一遍,計算以 $1$ 為根時的整個 DP 陣列。
接著再跑一遍 DFS,每次遇到一個 $u$ 的小孩 $v$ 可以在 $O(1)$ 的時間(只修改 dp[u] 和 dp[v])把 DP 陣列改成以 $v$ 為根,這樣我們就可以保證在遍歷到頂點 $u$ 的時候,整個 DP 陣列維護的是以 $u$ 為根對應的 DP 值。當然,要記得在離開 $v$ 之後撤銷這個改動,變回以 $u$ 為根的狀態。
在上面的論述中,我們假設了一個點拔掉一個小孩或是加上一個小孩之後 DP 值的變化可以快速算出來。在本題中,因為要模的數字 $M$ 不一定是一個質數(而且 $1 + dp_y$ 也可能是 $0$),所以我們不一定每次都可以除。一個常用的技巧是使用前綴和以及後綴和計算「去掉一個小孩之後的乘積」,這個技巧在取 max/min 類或是第 k 大之類的 DP 也可以用,基本上只要有結合律應該就可以想辦法組出來。以下是一個用這個想法完成的實做。
AC code : 前綴後綴和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
| #include <bits/stdc++.h>
using namespace std;
#define all(x) begin(x), end(x)
#ifdef CKISEKI
#include <experimental/iterator>
#define safe cerr<<__PRETTY_FUNCTION__<<" line "<<__LINE__<<" safe\n"
#define debug(a...) debug_(#a, a)
#define orange(a...) orange_(#a, a)
void debug_(auto s, auto ...a) {
cerr << "\e[1;32m(" << s << ") = (";
int f = 0;
(..., (cerr << (f++ ? ", " : "") << a));
cerr << ")\e[0m\n";
}
void orange_(auto s, auto L, auto R) {
cerr << "\e[1;33m[ " << s << " ] = [ ";
using namespace experimental;
copy(L, R, make_ostream_joiner(cerr, ", "));
cerr << " ]\e[0m\n";
}
#else
#define safe ((void)0)
#define debug(...) safe
#define orange(...) safe
#endif
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
int N, M;
cin >> N >> M;
vector<vector<int>> g(N);
for (int i = 1; i < N; i++) {
int u, v;
cin >> u >> v;
--u, --v;
g[u].push_back(v);
g[v].push_back(u);
}
auto mul = [&M](int64_t a, int64_t b) {
return static_cast<int>(a * b % M);
};
vector<int> dp(N), ans(N), pre(N), suf(N);
auto dfs = [&](auto &&self, int u, int pa) -> void {
dp[u] = 1;
for (int v : g[u]) {
if (v == pa) continue;
self(self, v, u);
dp[u] = mul(dp[u], 1 + dp[v]);
}
};
auto reroot = [&](auto &&self, int u, int pa) -> void {
ans[u] = dp[u];
// pre[v] 跟 suf[v] 代表從前面和從後面乘到 v 的積,
// 乘積裡不包含 v 這一格,而且 **會包含 pa**
{
int prod = 1;
for (int v : g[u]) {
pre[v] = prod;
prod = mul(prod, 1 + dp[v]);
}
}
{
int prod = 1;
for (int v : g[u] | views::reverse) {
suf[v] = prod;
prod = mul(prod, 1 + dp[v]);
}
}
for (int v : g[u]) {
if (v == pa) continue;
int orig_dpu = dp[u], orig_dpv = dp[v];
dp[u] = mul(pre[v], suf[v]);
dp[v] = mul(dp[v], 1 + dp[u]);
self(self, v, u);
dp[u] = orig_dpu;
dp[v] = orig_dpv;
}
};
dfs(dfs, 0, -1);
reroot(reroot, 0, -1);
for (int i = 0; i < N; i++)
cout << ans[i] << '\n';
}
|
另一種想法:下行與上行
另一種比較 pure 的解決本題的想法是這樣的。
我們改令兩個 DP 陣列 $down_u, up_u$。
$down_u$ 定義為「以 $1$ 為根時,$u$ 對應的子樹的塗色方法數,限制 $u$ 要是黑色」
基本上,$down_u$ 的定義和遞迴式和前面的作法的第一輪 DFS 求 $dp_u$ 都差不多。
$up_u$ 的定義則變成是「以 $1$ 為根時,$u$ 對應的 全方位子樹 的塗色方法數,限制 $pa_u$ 要是黑色」。這裡,$pa_u$ 是以 $1$ 為根時的 parent。而 全方位子樹 的意思是把整棵樹去掉 $u$ 對應的子樹的部份,也就是說那些不是 $u$ 的子孫的點。
每當遇到一個 $u$ 的小孩 $v$,$up_v$ 可以從 $up_u$ 以及 $u$ 除了 $v$ 以外的小孩的 $down$ 值推出來,大概就像下面畫的這樣:
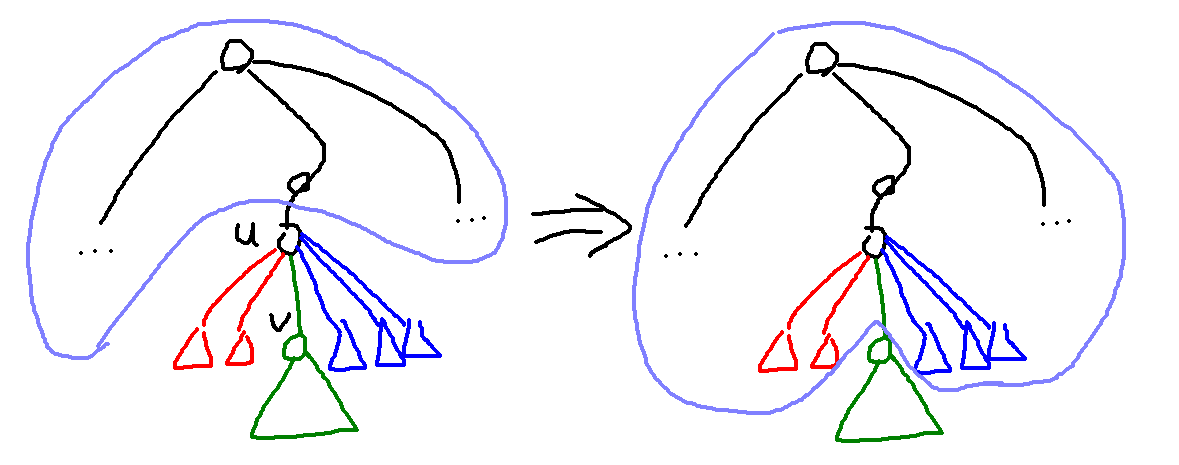
也就是說,我們可以遍歷兩次樹,第一次先從葉子開始從下往上計算 $down_u$,第二次則從樹根開始從上往下計算 $up_u$,得出所有 $up_u, down_u$ 之後我們可以把 $up_u, down_u$ 合在一起得出以 $u$ 為根時的答案,在本題的情況是 $(1 + up_u) \cdot down_u$。比較 tricky 的部份是我們要怎麼定樹根的 $up_u$:在本題中剛好定成 $0$ 可以讓樹根的小孩的 $up_u$ 都是對的,所以歸納地往下計算都是對的;在更一般的問題中,我們可能可以讓樹根的 $up_u$ 往下一層(本題對應到 $+1$)之後剛好變成 identity,或者乾脆不定義,直接對每個樹根的小孩都呼叫 calc_up。
AC code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
| #include <bits/stdc++.h>
using namespace std;
#define all(x) begin(x), end(x)
#ifdef CKISEKI
#include <experimental/iterator>
#define safe cerr<<__PRETTY_FUNCTION__<<" line "<<__LINE__<<" safe\n"
#define debug(a...) debug_(#a, a)
#define orange(a...) orange_(#a, a)
void debug_(auto s, auto ...a) {
cerr << "\e[1;32m(" << s << ") = (";
int f = 0;
(..., (cerr << (f++ ? ", " : "") << a));
cerr << ")\e[0m\n";
}
void orange_(auto s, auto L, auto R) {
cerr << "\e[1;33m[ " << s << " ] = [ ";
using namespace experimental;
copy(L, R, make_ostream_joiner(cerr, ", "));
cerr << " ]\e[0m\n";
}
#else
#define safe ((void)0)
#define debug(...) safe
#define orange(...) safe
#endif
signed main() {
cin.tie(nullptr)->sync_with_stdio(false);
int N, M;
cin >> N >> M;
vector<vector<int>> g(N);
for (int i = 1; i < N; i++) {
int u, v;
cin >> u >> v;
--u, --v;
g[u].push_back(v);
g[v].push_back(u);
}
auto mul = [&M](int64_t a, int64_t b) {
return static_cast<int>(a * b % M);
};
vector<int> pa(N);
vector<int> down(N);
auto calc_down = [&](auto &&self, int u) -> void {
down[u] = 1;
for (int v : g[u]) {
if (v == pa[u]) continue;
pa[v] = u;
self(self, v);
down[u] = mul(down[u], 1 + down[v]);
}
};
pa[0] = -1;
calc_down(calc_down, 0);
vector<int> pre(N), suf(N);
for (int u = 0; u < N; u++)
for (int prod = 1; int v : g[u]) {
if (v == pa[u]) continue;
pre[v] = prod;
prod = mul(prod, 1 + down[v]);
}
for (int u = 0; u < N; u++)
for (int prod = 1; int v : g[u] | views::reverse) {
if (v == pa[u]) continue;
suf[v] = prod;
prod = mul(prod, 1 + down[v]);
}
vector<int> up(N);
up[0] = 0;
auto calc_up = [&](auto &&self, int u) -> void {
for (int v : g[u]) {
if (v == pa[u]) continue;
up[v] = mul(1 + up[u], mul(pre[v], suf[v]));
self(self, v);
}
};
calc_up(calc_up, 0);
for (int i = 0; i < N; i++) {
int ans = mul(1 + up[i], down[i]);
cout << ans << '\n';
}
}
|
全方位子樹 這個名字我也不知道哪裡來的,只是感覺這樣叫很順。
參考資料與延伸閱讀

