TIOJ-1404

, ,

照亮的山景

https://tioj.ck.tp.edu.tw/problems/1404

Description

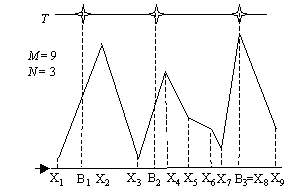
404 QQ
在一片山的上空，高度為$T$處有$N$個處於不同水平位置的燈泡，如上圖所示。
如果山的邊界上某一點與第$i$盞燈的連線不經過任何山稜線上的一點，我們稱第$i$盞燈可以照亮該點。
請問在所有$M$盞燈中，至少要打開幾盞燈，才能照亮山上每一個轉折點，或者打開所有的燈也無法照亮所有轉折點？

$1 \leq M, N \leq 10^5$
所有座標的絕對值小於$10^5$

Solution

發現到每個燈泡可以照到的範圍可能會長的非常奇怪
於是我們轉換思維，考慮每個轉折點如果要被照到要有什麼條件
可以發現，對於每個轉折點來說有一個區間，只要區間內有一個燈泡有開，這個轉折點就會被照到
找出那些區間之後這題就是經典的greedy題目了（按照右界由小到大，有拿過的跳過沒拿過的拿右界那個點）

那麼要怎麼找出這些區間呢？某個轉折點$p_i$對應的右界，正好是他和他右邊所有其他點所連出的射線中斜率最大者
維護一個上凸包能夠找到對應的那個點，再用直線求交點公式找出高度恰好是$T$的位置就好
左界也是同樣方式處理

因為題目給定的點已經幫我們排序好了，所以做凸包是$\mathcal{O}(M)$，而greedy的部分也可以做到$\mathcal{O}(N)$不過我這邊是放了$\mathcal{O}(N\log N)$的，因為找到交點之後必須二分搜求出到底涵蓋了哪些燈泡
總複雜度是$\mathcal{O}((M+N)\log N)$

AC code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

#include <bits/stdc++.h>
#define debug(x) cerr<<#x<<" = "<<x<<'\n'

using namespace std;
const int N = 100025;
signed main() {
    ios_base::sync_with_stdio(0), cin.tie(0);
    int m, n, T;
    while(cin >> m) {
        vector<pair<int,int>> v(m);
        for(auto &[x, y]: v) cin >> x >> y;
        cin >> n >> T;
        vector<int> bulb(n);
        for(int &x: bulb) cin >> x;
        vector<pair<int,int>> seg(m, pair<int,int>(0, n));

        {
            auto better = [](pair<int,int> a, pair<int,int> b, pair<int,int> c) {
                pair<int,int> AB(b.first-a.first, b.second-a.second);
                pair<int,int> BC(c.first-b.first, c.second-b.second);
                return 1LL * AB.first * BC.second - 1LL * BC.first * AB.second > 0;
            };
            vector<pair<int,int>> stk;
            for(int i = 0; i < m; i++) {
                while(stk.size() >= 2 && better(stk[stk.size()-2], stk[stk.size()-1], v[i]))
                    stk.pop_back();
                if(stk.size() && stk.back().second > v[i].second) {
                    double x = v[i].first + (T - v[i].second) * (stk.back().first - v[i].first) / double(stk.back().second - v[i].second);
                    seg[i].first = upper_bound(bulb.begin(), bulb.end(), x) - bulb.begin();
                }
                stk.push_back(v[i]);
            }
        }

        {
            auto better = [](pair<int,int> a, pair<int,int> b, pair<int,int> c) {
                pair<int,int> AB(b.first-a.first, b.second-a.second);
                pair<int,int> BC(c.first-b.first, c.second-b.second);
                return 1LL * AB.first * BC.second - 1LL * BC.first * AB.second < 0;
            };
            vector<pair<int,int>> stk;
            for(int i = m-1; i >= 0; i--) {
                while(stk.size() >= 2 && better(stk[stk.size()-2], stk[stk.size()-1], v[i]))
                    stk.pop_back();
                if(stk.size() && stk.back().second > v[i].second) {
                    double x = v[i].first + (T - v[i].second) * (stk.back().first - v[i].first) / double(stk.back().second - v[i].second);
                    seg[i].second = lower_bound(bulb.begin(), bulb.end(), x) - bulb.begin();
                }
                stk.push_back(v[i]);
            }
        }

        bool ok = true;
        for(int i = 0; i < m; i++) if(seg[i].first == seg[i].second) {
            cout << "you need more bulbs!\n";
            ok = false;
            break;
        }
        if(!ok) continue;
        sort(seg.begin(), seg.end(), [](pair<int,int> a, pair<int,int> b){return a.second < b.second;});
        int last = -1, ans = 0;
        for(auto [l, r]: seg) {
            if(l >= last) {
                last = r;
                ++ans;
            }
        }
        cout << ans << '\n';
    }
}
comments powered by Disqus