快樂規劃路徑
https://tioj.ck.tp.edu.tw/problems/1629
Description
樹朋友們生活在一個湖邊,湖邊的樹依照順時針方向編號為$1, 2, \dots n$。
他們想要讓自己更快樂,所以發明了一種娛樂方式,就是找到一條路徑遍歷全部$n$棵樹剛好一遍。
要從A樹到B樹唯一的方法就是架一條很長的梯子直直伸過去。
可是當然不是任何兩棵樹都可以架梯子,所以他們會先把所有可能架梯子的樹對(沒有錯字!)給你。
當然,(A,B)表示A可以到B、B也可以到A。
但是給定的遊歷路徑不能出現任兩條梯子交叉,不然可能會讓想要快樂的樹朋友發生危險。
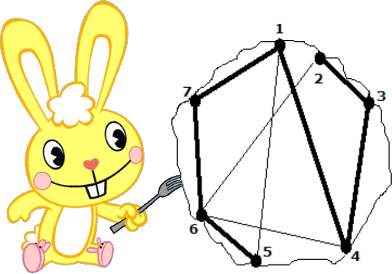
例如上圖粗線所示就是一個合法的快樂路徑。
給你樹的個數以及樹對,請輸出一組快樂路徑。
若有很多組解,樹朋友希望看到字典順序最小的那一組。
$5 \leq n \leq 1000$
Solution
由不能交叉的條件可以推出,在某個時刻已經遍歷過的點一定是環上的一個連續區間
所以可以2D/0D的區間DP,並記錄最小的轉移來源
我的dp$[i][L][0]$代表的是現在站在$i$,往順時鐘方向的$L$個都已經遍歷過了,$dp[i][L][1]$也相似只是換成逆時鐘
因為實在想不到更好的實作方式所以寫的有夠醜,但是只要好好選到最小的轉移來源就會是字典序最小的路徑了
AC code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| #include <bits/stdc++.h>
using namespace std;
const int N = 1025;
int n, m;
bool dp[N][N][2], fr[N][N][2], g[N][N];
signed main() {
ios_base::sync_with_stdio(0), cin.tie(0);
cin >> n >> m;
for(int i = 0; i < m; i++) {
int a, b;
cin >> a >> b, --a, --b;
g[a][b] = g[b][a] = true;
}
for(int i = 0; i < n; i++) dp[i][1][0] = dp[i][1][1] = true;
for(int L = 2; L <= n; L++) for(int i = 0; i < n; i++) {
// dp[i][L][0]
if(dp[(i+1)%n][L-1][0] && g[(i+1)%n][i]) { // (i+1)%n
fr[i][L][0] = 0;
dp[i][L][0] = true;
}
if(dp[(i+L-1)%n][L-1][1] && g[(i+L-1)%n][i]) { // (i+L-1)%n
if(!dp[i][L][0] || (i+1)%n > (i+L-1)%n)
fr[i][L][0] = 1;
dp[i][L][0] = true;
}
// dp[i][L][1]
if(dp[(i+n-1)%n][L-1][1] && g[(i+n-1)%n][i]) { // (i+n-1)%n
fr[i][L][1] = 0;
dp[i][L][1] = true;
}
if(dp[(i+n+1-L)%n][L-1][0] && g[(i+n+1-L)%n][i]) { // (i+n+1-L)%n
if(!dp[i][L][1] || (i+n-1)%n > (i+n+1-L)%n)
fr[i][L][1] = 1;
dp[i][L][1] = true;
}
}
for(int i = 0; i < n; i++) {
if(dp[i][n][0] || dp[i][n][1]) {
vector<int> ans;
for(int c = 0; c < 2; c++) if(dp[i][n][c]) {
int d = c;
vector<int> vv;
for(int L = n; L >= 1; L--) {
vv.push_back(i);
// cerr<<dp[i][L][d]<<',';
int f = fr[i][L][d];
if(d) {
if(f) {
i = (i+n+1-L)%n;
d = 0;
}else {
i = (i+n-1)%n;
d = 1;
}
}else {
if(f) {
i = (i+L-1)%n;
d = 1;
}else {
i = (i+1)%n;
d = 0;
}
}
}
if(ans.empty() || vv < ans) ans = vv;
}
for(int x: ans) cout << x+1 << '\n';
return 0;
}
}
cout << -1 << '\n';
}
|
