FFT-NTT

,

捲積方法 OAO

本篇的重點應該是放在理解與使用與競程相關的捲積，其中會利用到FFT或NTT加速
這邊先定義一下捲積$ * $是什麼

$$
(a * b) _ x = \sum _ {i+j=x} a_i b_j
$$

實際上就等價於我們常見的多項式乘法
naive的做法是$\mathcal{O}(n^2)$，顯然不夠令人滿意

1
2
3
4
5

for(int i = 0; i < A.size(); i++) {
	for(int j = 0; j < B.size(); j++) {
		res[i+j] += A[i] * B[j];
	}
}

DFT

先假設我們有兩個多項式
$$
A(x) = \sum a_i x^i, B(x) = \sum b_i x^i\newline
C(x) = A(x)B(x)
$$
除了上述利用分配律乘開以外
因為$C$的次數已經可以確定
我們也可以在$A(x)$和$B(x)$找出$n$個相異的點，相乘之後再利用插值法代入得到$C$
其中$n = \deg C + 1$
也就是

$$
\begin{bmatrix}
1 & x_0 & x_0^2 & \cdots & x_0^{n-1}\newline
1 & x_1 & x_1^2 & \cdots & x_1^{n-1}\newline
\vdots & \vdots & \vdots & \ddots & \vdots\newline
1 & x _ {n-1} & x _ {n-1}^2 & \cdots & x _ {n-1}^{n-1}
\end{bmatrix}
\begin{bmatrix}
a_0\newline a_1\newline \vdots\newline a _ {n-1}
\end{bmatrix} =
\begin{bmatrix}
A(x_0)\newline A(x_1)\newline \vdots\newline A(x _ {n-1})
\end{bmatrix}
$$

$$
\begin{bmatrix}
1 & x_0 & x_0^2 & \cdots & x_0^{n-1}\newline
1 & x_1 & x_1^2 & \cdots & x_1^{n-1}\newline
\vdots & \vdots & \vdots & \ddots & \vdots\newline
1 & x _ {n-1} & x _ {n-1}^2 & \cdots & x _ {n-1}^{n-1}
\end{bmatrix}
\begin{bmatrix}
b_0\newline b_1\newline \vdots\newline b _ {n-1}
\end{bmatrix} =
\begin{bmatrix}
B(x_0)\newline B(x_1)\newline \vdots\newline B(x _ {n-1})
\end{bmatrix}
$$

$$
\begin{bmatrix}
1 & x_0 & x_0^2 & \cdots & x_0^{n-1}\newline
1 & x_1 & x_1^2 & \cdots & x_1^{n-1}\newline
\vdots & \vdots & \vdots & \ddots & \vdots\newline
1 & x _ {n-1} & x _ {n-1}^2 & \cdots & x _ {n-1}^{n-1}
\end{bmatrix}
^{-1}
\begin{bmatrix}
A(x_0)B(x_0)\newline A(x_1)B(x_1)\newline \vdots\newline A(x _ {n-1})B(x _ {n-1})
\end{bmatrix} =
\begin{bmatrix}
c_0\newline c_1\newline \vdots\newline c _ {n-1}
\end{bmatrix}
$$

最後一步直接高斯消去或用拉格朗日/牛頓插值法可以做到$\mathcal{O}(n^2)$

上述步驟稱為DFT(對序列的版本叫離散傅立葉變換，與使用積分的連續傅立葉變換相對)和IDFT
但是這樣根本沒有改進多少複雜度啊？
邁向快速傅立葉變換的鑰匙是利用複數，取特定的某些$x$讓我們能夠分治

Root of Unity

首先先來介紹單位根$\omega$是使得

$$
\omega ^ n = 1\newline
\forall 0 \leq i < j < n, \omega^i \neq \omega^j
$$

的數

複習一下歐拉公式$$e^{ix} = \cos x + i\sin x$$
習慣上可以取$\omega_n = e^{-\frac{2\pi i}{n}}$(下標是表示$n$是最小的$i$使$\omega^i = 1$，或者說$\operatorname{ord}(\omega_n) = n$)

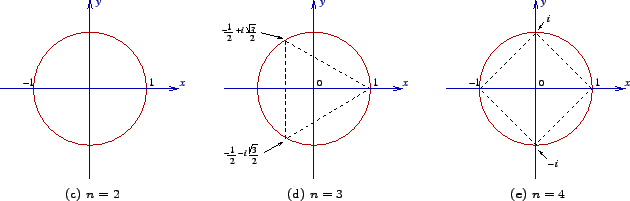
404的啦QQ

推薦觀賞3B1B系列
https://youtu.be/v0YEaeIClKY
https://youtu.be/mvmuCPvRoWQ

引理們

Lemma a.

$$
\omega _ {dn}^{dk} = (e^{\frac{2\pi i}{dn}})^{dk} = (e^{\frac{2\pi i}{n}})^k = \omega_n^k
$$

Lemma b.

$$
\omega_n^{\frac{n}{2}} = \omega_2 = e^{i\pi} = -1
$$

Cooley-Tukey FFT algorithm

先假設$n$是2的冪次，然後下面提到的$i$都只是index
將DFT中的$x_i$取值為$\omega_n^i$，可以知道我們要算的就是對$i \in [0, n-1]$求
$$
y_i = \sum _ {j=0}^{n-1} a_j (\omega_n^i)^j
$$
把右式的奇數項和偶數項分開處理(這邊是原理的精華)
$$
\begin{align}
y_i = \sum _ {j=0}^{n-1} a_j (\omega_n^i)^j
&= \sum _ {j=0}^{\frac{n}{2}-1} a _ {2j} (\omega_n^i)^{2j} + \sum _ {j=0}^{\frac{n}{2}-1} a _ {2j+1} (\omega_n^i)^{2j+1}\newline
&= \sum _ {j=0}^{\frac{n}{2}-1} a _ {2j} (\omega _ {\frac{n}{2}}^i)^j + \omega_n^i \sum _ {j=0}^{\frac{n}{2}-1} a _ {2j+1} (\omega _ {\frac{n}{2}}^i)^j\newline
&= F _ {even}(i) + \omega_n^i F _ {odd}(i)
\end{align}
$$

其中$F _ {even}, F _ {odd}$分別是以奇數和偶數項FFT得到的東西，可以遞迴求解
雖然以$\frac{n}{2}$的長度遞迴只能得到$i \in [0, \frac{n}{2}-1]$的答案
不過$F _ {even}$和$F _ {odd}$都有週期$\frac{n}{2}$，再由Lemma b.可以簡化成

$$
\text{for } 0 \leq i < \frac{n}{2},
\left\{\begin{matrix}
y _ i &= F _ {even}(i) + \omega_n^i F _ {odd}(i) \newline
y _ {i+\frac{n}{2}} &= F _ {even}(i) - \omega_n^i F _ {odd}(i)
\end{matrix}\right.
$$

時間複雜度有$T(n) = 2T(n/2) + \mathcal{O}(n)$，由主定理可知$T(n) = \mathcal{O}(n\log n)$
要將FFT一言以概之，大概就是利用分治法將多項式轉換成點值表示吧
附上遞迴版的參考程式碼，雖然迭代版通常效率較好不過遞迴版有助於理解

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

const double PI = acos(-1);
typedef complex<double> cd;
vector<cd> FFT(const vector<cd> &F) { // assume F.size() == 2^k
	if(F.size() == 1) return F; // base case (important)
	vector<cd> rec[2], ans;
	for(int i = 0; i < F.size(); i++) rec[i&1].push_back(F[i]);
	rec[0] = FFT(rec[0]);
	rec[1] = FFT(rec[1]);
	double theta = -2*PI / F.size();
	cd now = 1, omega(cos(theta), sin(theta));
	ans.resize(F.size());
	for(int i = 0; i < F.size()/2; i++) {
		ans[i] = rec[0] + now * rec[1];
		ans[i+F.size()/2] = rec[0] - now * rec[1];
	}
	return ans;
}

Inverse-FFT

那麼要怎麼做IFFT(傅立葉變換的逆變換)，也就是把點值表示轉換回係數呢？
FFT可以寫成矩陣的形式，也就是

$$
\begin{bmatrix}
1 & 1 & 1 & \cdots & 1\newline
1 & \omega & \omega^2 & \cdots & \omega^{n-1}\newline
\vdots & \vdots & \vdots & \ddots & \vdots\newline
1 & \omega^{n-1} & (\omega^{n-1})^2 & \cdots & (\omega^{n-1})^{n-1}
\end{bmatrix}
\begin{bmatrix}
c_0\newline c_1\newline \vdots\newline c _ {n-1}
\end{bmatrix} =
\begin{bmatrix}
C(1)\newline C(\omega)\newline \vdots\newline C(\omega^{n-1})
\end{bmatrix}
$$
左項有一個范德蒙矩陣$V = [\omega^{ij}]$ (0-base)
事實上其反矩陣就是$V’ = [\frac{1}{n}\omega^{-ij}]$

說明:
$$
[V * V’] _ {i,j} = \sum _ {k=0}^{n-1} V _ {i,k} V’ _ {k,j} = \frac{1}{n}\sum _ {k=0}^{n-1} \omega^{k(i-j)}
$$
$i=j$時顯然為1
當$i \neq j$利用等比級數公式可以知道總和為$0$
故相乘的結果是單位矩陣

可以發現我們只需要把FFT的$\omega$改成倒數，最後再除上$n$就是IFFT所需要的
因為FFT和IFFT的相似性，我們可以將程式碼整合如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

const double PI = acos(-1);
typedef complex<double> cd;
vector<cd> FFT(const vector<cd> &F, bool inv) { // assume F.size() == 2^k
	if(F.size() == 1) return F; // base case (important)
	vector<cd> rec[2];
	for(int i = 0; i < F.size(); i++) rec[i&1].push_back(F[i]);
	rec[0] = FFT(rec[0],inv);
	rec[1] = FFT(rec[1],inv);
	double theta = (inv ? 1 : -1) * 2 * PI / F.size();
	cd now = 1, omega(cos(theta), sin(theta));
	vector<cd> ans(F.size());
	for(int i = 0; i < F.size()/2; i++) {
		ans[i] = rec[0][i] + now * rec[1][i];
		ans[i+F.size()/2] = rec[0][i] - now * rec[1][i];
		now *= omega;
	}
	if(inv) for(int i = 0; i < ans.size(); i++) ans[i] /= 2;
	return ans;
}

Convolution

有了FFT和IFFT兩個工具，我們要做捲積就很簡單了

  1. 確定兩個多項式相乘的次數，並且選擇一個足夠大的$n = 2^k$(後面可以補0)
  2. 利用Cooley-Tukey演算法求出$A,B$的傅立葉變換$\hat A, \hat B$
  3. 將$\hat A, \hat B$在對應位置兩兩相乘得到$\hat C$(可能叫Hadamard Product吧)
  4. 再利用Cooley-Tukey演算法求出$C$
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

vector<cd> A{1,3,4};
vector<cd> B{1,2,5};
signed main() {
    int n = 1<<__lg(A.size()+B.size())+1;
    A.resize(n);
    B.resize(n);
    A = FFT(A,0);
    B = FFT(B,0);
    vector<cd> C(n);
    for(int i = 0; i < n; i++) C[i] = A[i]*B[i];
    C = FFT(C,1);
    for(int i = 0; i < n; i++) cout << C[i].real() << " \n"[i==n-1];
}

Iterative Version

迭代的版本不但簡單執行時間又快，值得記一下

觀察遞迴的情況
可以看到我們每次都是將一個序列的偶數項放前面做，奇數項放後面做再合併
這可以想成將最低位的0/1移到最高位，例如
$$
100010\textbf{1} \rightarrow \textbf{1}100010\newline
111110\textbf{1} \rightarrow \textbf{1}111110\newline
101010\textbf{0} \rightarrow \textbf{0}101010
$$
重複執行了把最低位移到最高位的動作$k = \log_2{n}$次之後
原本放在$i$的位置的數字的index最後會被放到$j$的地方，其中$j$是$i$在$k$位二進位數的反轉
也就是說我們可以一開始就把所有數字放到他在遞迴樹中對應的位置，再一層一層往上合併

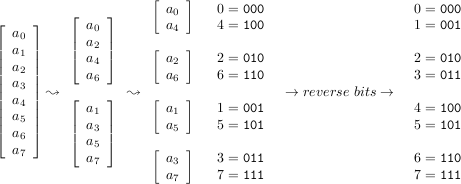
404的啦QQ

那要拿哪些合併呢？其實每個相鄰的兩塊的相同位置對應的就是$F _ {even}$和$F _ {odd}$，組合算出$y_i$之後要填的地方也是那兩格
剩下的就是看code理解了吧…OwO?

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

typedef complex<double> cd;
void FFT(cd F[], int n, bool inv) { // in-place FFT, also assume n = 2^k
	for(int i = 0, j = 0; i < n; i++) {
		if(i < j) swap(F[i], F[j]);
		// magic! (maintain j to be the bit reverse of i)
		for(int k = n>>1; (j^=k) < k; k>>=1);
	}
	for(int step = 1; step < n; step <<= 1) {
		double theta = (inv ? 1 : -1) * PI / step;
		cd omega(cos(theta), sin(theta));
		for(int i = 0; i < n; i += step*2) {
			cd now(1,0);
			for(int j = 0; j < step; j++) {
				cd a = F[i+j];
				cd b = F[i+j+step] * now;
				F[i+j] = a+b;
				F[i+j+step] = a-b;
				now *= omega;
			}
		}
	}
	if(inv) for(int i = 0; i < n; i++) F[i] /= n;
}

NTT

注意到我們可以實行分治的關鍵就是存在一個$\omega$使得

$$
\omega ^ n = 1 \wedge
\forall 0 \leq i < j < n, \omega^i \neq \omega^j
$$

現在我們想要在模一個質數$p$下做類似的事

費馬小定理表明

$$
\forall (a,p) = 1, a^{\varphi(p)} \equiv 1 \pmod p
$$

如果有原根$g$使得

$$
\forall 0 \leq i < j < \varphi(p), g^i \not \equiv g^j \pmod p
$$

那麼$\omega$的選擇就很簡單了，也就是$\omega_n \equiv g ^ {\frac{\varphi(p)}{n}}$
容易驗證$\omega_n$滿足上面的性質

這樣做必須滿足$n | \varphi(p)$，而若使用Cooley-Tukey演算法的話$n$會是2的冪次
也就是說若$\varphi(p) = p-1 = t \cdot 2^k$，其中$t$是奇數
那對這個$p$來說可行的$n$的範圍最多就是$2^k$了
這也是為什麼NTT的模數常常都是那些數字的原因
因為$p-1$必須在二進位下有很多個後綴0

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

const int64_t MOD = 998244353, G = 3;
int64_t modpow(int64_t e, int64_t p, int64_t m) {
	int64_t r = 1;
	for(; p; p>>=1) {
		if(p&1) r = r*e%m;
		e = e*e%m;
	}
	return r;
}
void NTT(int64_t F[], int n, bool inv) { // assume n = 2^k!
	for(int i = 0, j = 0; i < n; i++) {
		if(i < j) swap(F[i], F[j]);
		for(int k = n>>1; (j^=k) < k; k>>=1);
	}
	for(int step = 1; step < n; step <<= 1) {
		//may preprocess to boost
		int64_t omega = modpow(G, (MOD-1) / (step*2), MOD);
		if(inv) omega = modpow(omega, MOD-2, MOD);
		for(int i = 0; i < n; i += step*2) {
			int64_t now = 1;
			for(int j = 0; j < step; j++) {
				cd a = F[i+j];
				cd b = F[i+j+step] * now % MOD;
				// reduce the use of % operator
				F[i+j] = (a+b < MOD ? a+b : a+b-MOD);
				F[i+j+step] = (a-b<0 ? a-b+MOD : a-b);
				now = now*omega%MOD;
			}
		}
	}
	if(inv) {
		int64_t invn = modpow(n, MOD-2, MOD);
		for(int i = 0; i < n; i++) F[i] = F[i]*invn%MOD;
	}
}

→NTT模數表←

中國剩餘?

一個模數合不合適取決於最後答案的大小
兩個值域$c$、長度$n$的多項式相乘，得出來的乘積的值域最多會是$nc^2$
如果不會超過模數的話就可以直接使用
但如果會超過怎麼辦？
挑選更大的模數沒什麼用，因為相乘起來可能就超過long long了
這時我們就必須做多次NTT再用中國剩餘定理合併

如果真實的答案不是指數或階乘那種直接爆炸的數值
甚至還可以用來對任意數字取模(?)

End

FFT與NTT的利用其實滿少的，大部分不是大數乘法就是生成函數，以後有時間再放一篇講好了

comments powered by Disqus