迭代式線段樹
先備知識: 線段樹(帶懶標) + 位元運算(吧)
如果讀者還不知道線段樹的原理最好看遞迴的(?)
單點修改
例題仍然是萬年RMQ
給定一個長度$n$的序列,請支援以下操作
- 將位置$p$的值改為$x$
- 查詢區間$[l,r)$的最大值
完美二元樹
首先假定$n$是2的冪次,思考可能可以簡單一些
我們一樣用1當根,並且節點i的左右子樹會是i*2和i*2+1或寫成i<<1, i<<1|1
1
2
| const int N = 1<<18;
int tr[N<<1], n;
|
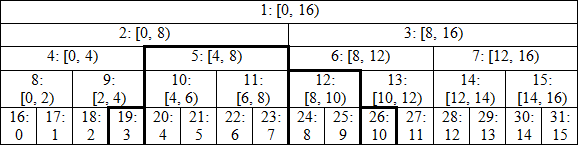
對於初始化來說,可以發現葉子節點對應的都是長度$1$的區間,正好是原序列的值,所以可以直接讀入或另外傳入賦值給 tr[i+n],接著可以用遞減的順序把其他長度的區間的答案算好
1
2
3
4
| void build(int v[]) {
for(int i = 0; i < n; i++) tr[i+n] = v[i];
for(int i = n-1; i > 0; i--) tr[i] = max(tr[i<<1], tr[i<<1|1]);
}
|
更新一個節點$p$,那麼只有$p$的所有祖先的答案會被影響到
注意 p^1 代表 p 的兄弟節點,也就是 p 父親的另一個兒子
1
2
3
4
| void modify(int p, int x) {
for(tr[p+=n] = x; p > 1; p>>=1)
tr[p>>1] = max(tr[p],tr[p^1]);
}
|
至於區間的查詢就沒有那麼顯然了,我們一樣必須把詢問的區間拆分成線段樹上的一些區間,而且數量不能超過$\mathcal{O}(\log n)$
事實上,每一層我們至多只會拿前後兩個節點,並且拿完了之後就把左界增加或右界減少,越往上待選節點所代表區間會越短
如果採用左閉右開的話規則可以歸納如下:
- 首先
l+=n, r+=n 從最下面那層開始 - 重複執行直到區間為空(
l>=r)- 如果
l 是他父親的右子樹,則必須取走編號 l 的節點,並將 l 在該層往右一格 - 如果
r-1 是他父親的左子樹,則必須取走編號 r-1 的節點,並將 r 在該層往左一格 - 把
l,r 都往上提升一層
1
2
3
4
5
6
7
8
| int query(int l, int r) { // [l,r)
int res = -1e9;
for(l+=n,r+=n; l<r; l>>=1,r>>=1) {
if(l&1) res = max(res, tr[l++]);
if(r&1) res = max(res, tr[--r]);
}
return res;
}
|
嗯…如果看不懂的話也可以接受這就是把$[l,r)$區間拆成線段樹上$2\log n$個節點就好
和那些噁心的遞迴參數say goodbye吧! \迭代式線段樹/
如果n不是2的冪次?
如果題目需要的運算有單位元素的話,可以在後面補上單位元素直到n是2的冪次
不過令人意外的是, 上面的程式碼對任意的n都正確!
讓我們來看看 n = 13 的例子
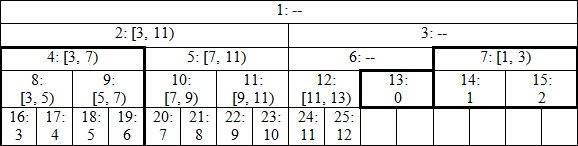
現在它不是一棵完美二元樹了,而是很多棵: 以 2 為根高度4的、以 13 為根高度1的、以 7 為根高度2的
畫上底線的節點在 query 的時候不會被動到,所以實際上它們是什麼值都沒有差
n不是2的冪次的時候這個演算法仍然正確的原因,可能是它可以被證明和另一個更大二元樹同構吧,不過我也不會證明所以請讀者自己參透(X)
不把n提高到2的冪次,除了讓程式碼更好看之外,空間使用量也從 $4n$ 減少到了 $2n$
不過同時也有一些缺點,例如不好在線段樹上二分搜,沒有 1 號節點代表全域的答案等等(如果沒有交換律)
不遵守交換律的區間查詢?
其實這很容易解決,直接上code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| node query(int l, int r) {
node resl, resr; // initialized as identity
for(l+=n,r+=n; l<r; l>>=1,r>>=1) {
if(l&1) resl = combine(resl, tr[l++]);
if(r&1) resr = combine(tr[--r], resr);
}
return combine(resl, resr);
}
void pull(int p) {
while(p > 1) {
p >>= 1;
tr[p] = combine(tr[p<<1],tr[p<<1|1])
tr[p] = applyTag(tr[p], tag[p]);
}
}
|
畢竟區間 query 的原理就是拿每一層前後的區間,所以只要對前後分開存就好了
應王勻的要求把 pull 也補上,因為沒有交換律的時候不能用 combine(tr[p], tr[p^1]) @@
什麼? 你問我沒有結合律怎麼辦?
一個小常識是線段樹必須滿足結合律才能使用……
迭代型線段樹 with 懶標
進到了大家最需要,也是最常寫爛的部分了owo
zkw自己似乎是喜歡差分、懶標永久化之類的寫法,不過太精妙了先不解釋XD
現在題目的單點修改操作變成了區間修改
- 把區間$[l,r)$的數字都增加$x$
首先我們需要額外的陣列代表懶標,而其長度只需要n,因為葉子節點不需再往下傳遞懶標
Helper Methods
區間修改時,我們就在存取到的那些節點的答案和懶標都加上$x$,因此有了
1
2
3
4
| void upd(int p, int x) {
tr[p] += x;
if(p < n) tag[p] += x;
}
|
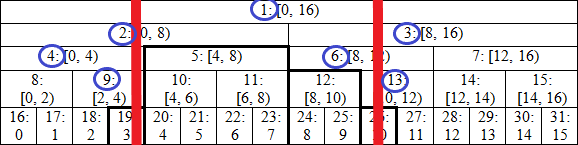
再看一次這張圖,可以想像有兩條分別通過 l 和 r-1 的垂直線,這條線通過的節點是懶標會影響到目前區間答案的節點,所以必須把懶標往下傳
順序要由上而下,把 p 的祖先節點的懶標往下推
細節請看code
1
2
3
4
5
6
7
8
9
| void push(int p) {
for(int h = __lg(n); h >= 0; h--) {
int i = p>>h; // hth ancestor of p
if(!tag[i>>1]) continue;
upd(i, tag[i>>1]);
upd(i^1, tag[i>>1]);
tag[i>>1] = 0;
}
}
|
另外修改之後也同樣需要對 l 和 r-1 的祖先 pull ,順序要由下而上
1
2
3
4
5
6
7
| void pull(int p) {
while(p > 1) {
// do not forget the tag[p>>1] term
tr[p>>1] = max(tr[p],tr[p^1])+tag[p>>1];
p >>= 1;
}
}
|
Lazy Propagation!
寫好這兩個函式後,區間修改就不是難事啦
別忘了:
query 前要 pushmodify 前要 push , modify 後要 pull
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| int query(int l,int r) {
push(l+n), push(r-1+n);
int res = -1e9;
for(l+=n,r+=n; l<r; l>>=1,r>>=1) {
if(l&1) res = max(res, tr[l++]);
if(r&1) res = max(res, tr[--r]);
}
return res;
}
void modify(int l,int r, int d) {
int tl = l, tr = r;
push(l+n), push(r-1+n);
for(l+=n,r+=n; l<r; l>>=1,r>>=1) {
if(l&1) upd(l++, d);
if(r&1) upd(--r, d);
}
// uses tl,tr here for l,r changed
pull(tl+n), pull(tr-1+n);
}
|
全都是同一個框架,實在是舒服啊!
除非時間先後順序會影響到所需的運算,例如同時有乘值和加值兩種操作,否則 modify 前可以不用 push
區間和
有人可能想到了,有些懶標操作需要區間長度,例如區間加值區間和,怎麼辦呢?
所有節點代表的區間長度都是2的冪次,也和它與葉子的距離有關
只需修改一下便可
以下順便附上完整的區間加值區間和的程式碼,以筆者習慣的風格撰寫
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| const int N = 200000;
struct segtree {
long long sum[N<<1], tag[N], n;
void upd(int p, long long d, int h) {
sum[p] += d<<h;
if(p < n) tag[p] += d;
}
void pull(int p) {
for(int h=1; p>1; p>>=1, h++) sum[p>>1] = sum[p^1]+sum[p] + (tag[p>>1]<<h);
}
void push(int p) {
for(int h = __lg(n); h >= 0; h--) {
int i = p>>h;
if(!tag[i>>1]) continue;
upd(i,tag[i>>1],h);
upd(i^1,tag[i>>1],h);
tag[i>>1] = 0;
}
}
void add(int l,int r,long long k) {
int tl = l, tr = r, h = 0;
push(l+n), push(r-1+n);
for(l+=n, r+=n; l<r; l>>=1, r>>=1, h++) {
if(l&1) upd(l++,k,h);
if(r&1) upd(--r,k,h);
}
pull(tl+n), pull(tr-1+n);
}
long long query(int l,int r) { // [l,r)
long long res = 0;
push(l+n), push(r-1+n);
for(l+=n, r+=n; l<r; l>>=1, r>>=1) {
if(l&1) res += sum[l++];
if(r&1) res += sum[--r];
}
return res;
}
void init(long long v[],int _n) {
n = _n;
for(int i = 0; i < n; i++) sum[i+n] = v[i];
for(int i = n-1; i > 0; i--) sum[i] = sum[i<<1]+sum[i<<1|1];
}
} sgt;
|
參考資料
https://codeforces.com/blog/entry/18051
寫這篇好久ㄛ,本來想寫全國模擬賽的題解,不過既然學長都給了我還是算了吧(汗)


